Advertisements
Advertisements
Question
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
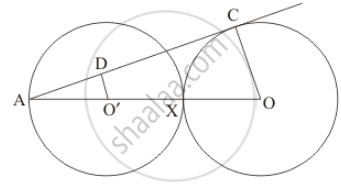
Solution
Consider the two triangles Δ ADOand Δ ACO.

We have,
∠ A is a common angle for both the triangles.
`∠ ADO =90^o` (Given in the problem)
`∠ ACO = 90^o` (Since OC is the radius and AC is the tangent to that circle at C and we know that the radius is always perpendicular to the tangent at the point of contact)
Therefore,
`∠ ADO = ∠ACO`
From AA similarity postulate we can say that,
Δ ACO ~ Δ ADO
Since the triangles are similar, all sides of one triangle will be in same proportion to the corresponding sides of the other triangle.
Consider AO′ of Δ ADO and AO of Δ ACO .
`(AO)/(AO)=(AO)/(AO+OX+OX)`
Since AO′ and O′X are the radii of the same circle, we have,
AO′ = O′X
Also, since the two circles are equal, the radii of the two circles will be equal. Therefore,
AO′ = XO
Therefore we have
`(AO)/(AO)=(AO)/(AO+AO+AO)`
`(AO)/(AO)=1/3`
Since Δ ACO ~ Δ ADO,
`(AO)/(AO)=(DO)/(CO)`
We have found that,
`(AO)/(AO)=1/3`
Therefore,
`(DO)/(CO)=1/3`
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
An equilateral triangle ABC is inscribed in a circle with centre O. The measures of ∠BOCis
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
From the figure, identify a sector.

