Advertisements
Advertisements
Question
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Solution
In the given figure,
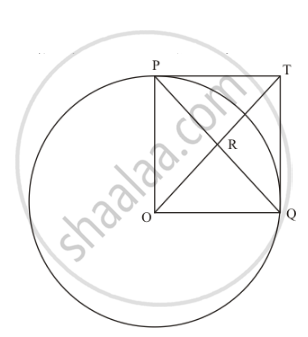
PO = OQ (Since they are the radii of the same circle)
PT = TQ (Length of the tangents from an external point to the circle will be equal) Now considering the angles of the quadrilateral PTQO, we have,
`∠POQ=90^o` (Given in the problem)
`∠OPT=90^o` (The radius of the circle will be perpendicular to the tangent at the point of contact)
`∠ TQO=90^o` (The radius of the circle will be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,
`∠ POQ+∠TQO+∠OPT+∠PTQ=360^o`
`90^O+90^O+90^O+∠ PTQ=360^o`
`∠ PTQ=90^o`
Thus we have found that all angles of the quadrilateral are equal to 90°.
Since all angles of the quadrilateral PTQO are equal to 90° and the adjacent sides are equal, this quadrilateral is a square.
We know that in a square, the diagonals will bisect each other at right angles.
Therefore, PQ and OT bisect each other at right angles.
Thus we have proved.
APPEARS IN
RELATED QUESTIONS
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
ture or false v
The degree measure of a semi-circle is 180°.
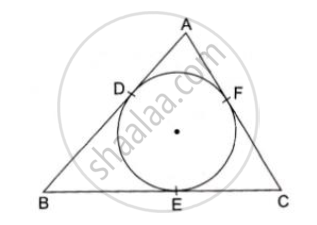
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
One chord of a circle is known to be 10 cm. The radius of this circle must be
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
ABC is a right triangle in which ∠B = 90°. If AB = 8 cm and BC = 6 cm, find the diameter of the circle inscribed in the triangle.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
The length of tangent from an external point on a circle is always greater than the radius of the circle.
In the given figure, O is the centre of the circle. Name all radii of the circle.