Advertisements
Advertisements
Question
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
Solution
It is given that, AB as diameter, O is centre and`angle CAB = 30°`
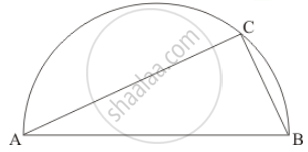
We have to find `m angleACB` and ` m angleABC`
Since angle in a semi-circle is a right angle therefore
`angleACB = 90°`
In Δ ACD we have
`angleCAB` = 30° (Given)
`angleACB `= 90° (Angle in semi-circle is right angle)
Now in Δ ACB we have
`angleCAB + angleACB + angleABC `= 180
`angleABC = 180° - (angle CAB + angleCAB )`
=180° - (90° + 30° )
= 180° - 120°
= 60°
Hence `angle ABC = 60°` and `angleACB = 90°`
APPEARS IN
RELATED QUESTIONS
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
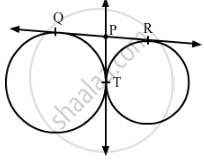
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
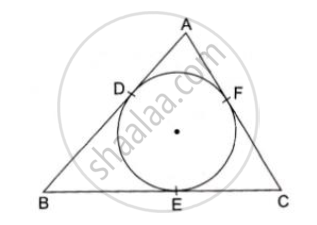
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

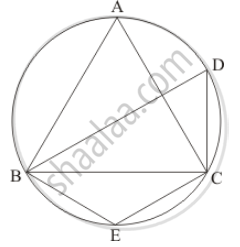
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
