Advertisements
Advertisements
Question
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

Solution
Construction: Join OA,OB,OC,OE ⊥ AB at E and OF ⊥ AC at F

We know that tangent segments to a circle from me same external point are congruent
Now, we have
AE = AF, BD = BE =6 cm and CD = CF = 9 cm
Now,
Area(ΔABc) = Area ( ΔBOC)+ Area( ΔAOB) +Area( ΔAOC)
`⇒ 54 = 1/2 xx BC xx OD + 1/2 AB xx OE + 1/2 xx AC xx OF `
⇒ 108 = 15 × 3+(6+x) ×3 +(9+x) × 3
⇒ 36=15+6+x+9+x
⇒ 36=30+2x
⇒ 2x = 6
⇒ x = 3 cm
∴ AB =6+3=9 cm and AC =9+3=12cm
APPEARS IN
RELATED QUESTIONS
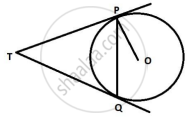
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

A line segment joining any point on the circle to its center is called the _____________ of the circle
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]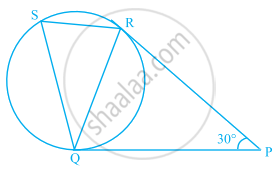
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.