Advertisements
Advertisements
Question
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Solution
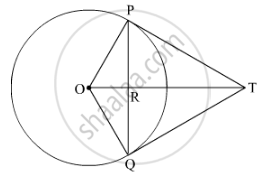
TP and TQ are tangents drawn from an external point T to the circle. O is the centre of the circle.
Suppose OT intersect PQ at point R.
In ∆OPT and ∆OQT,
OP = OQ (Radii of the circle)
TP = TQ (Lengths of tangents drawn from an external point to a circle are equal.)
OT = OT (Common sides)
∴ ∆OPT ≅ ∆OQT (By SSS congruence rule)
So, ∠PTO = ∠QTO (By CPCT) .....(1)
Now, in ∆PRT and ∆QRT,
TP = TQ (Lengths of tangents drawn from an external point to a circle are equal.)
∠PTO = ∠QTO [From (1)]
RT = RT (Common sides)
∴ ∆PRT ≅ ∆QRT (By SAS congruence rule)
So, PR = QR .....(2) (By CPCT)
And, ∠PRT = ∠QRT (By CPCT)
Now,
∠PRT + ∠QRT = 180° (Linear pair)
⇒ 2∠PRT = 180°
⇒ ∠PRT = 90°
∴ ∠PRT = ∠QRT = 90° .....(3)
From (2) and (3), we can conclude that
OT is the right bisector of the line segment PQ.
APPEARS IN
RELATED QUESTIONS
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In the given figure, if ∠ABC = 45°, then ∠AOC =
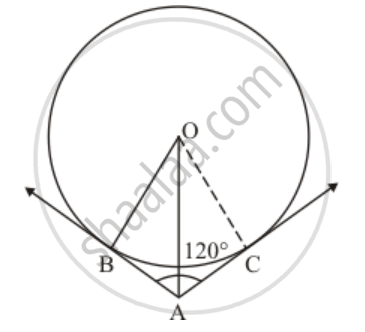
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
In the following figure, BC is a diameter of the circle and ∠BAO = 60º. Then ∠ADC is equal to ______.
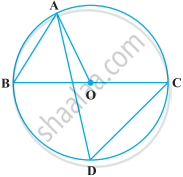
In the given figure, O is the centre of the circle. Name all chords of the circle.