Advertisements
Advertisements
प्रश्न
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
उत्तर
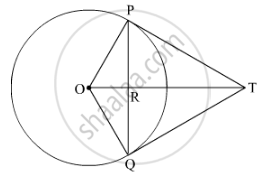
TP and TQ are tangents drawn from an external point T to the circle. O is the centre of the circle.
Suppose OT intersect PQ at point R.
In ∆OPT and ∆OQT,
OP = OQ (Radii of the circle)
TP = TQ (Lengths of tangents drawn from an external point to a circle are equal.)
OT = OT (Common sides)
∴ ∆OPT ≅ ∆OQT (By SSS congruence rule)
So, ∠PTO = ∠QTO (By CPCT) .....(1)
Now, in ∆PRT and ∆QRT,
TP = TQ (Lengths of tangents drawn from an external point to a circle are equal.)
∠PTO = ∠QTO [From (1)]
RT = RT (Common sides)
∴ ∆PRT ≅ ∆QRT (By SAS congruence rule)
So, PR = QR .....(2) (By CPCT)
And, ∠PRT = ∠QRT (By CPCT)
Now,
∠PRT + ∠QRT = 180° (Linear pair)
⇒ 2∠PRT = 180°
⇒ ∠PRT = 90°
∴ ∠PRT = ∠QRT = 90° .....(3)
From (2) and (3), we can conclude that
OT is the right bisector of the line segment PQ.
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

true or false
The degree measure of an arc is the complement of the central angle containing the arc.
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
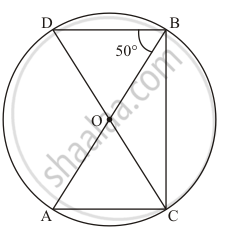
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Draw a circle of any radius. Show one diameter, one radius and one chord on that circle.
Twice the radius is ________________
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
Say true or false:
Two diameters of a circle will necessarily intersect.
