Advertisements
Advertisements
प्रश्न
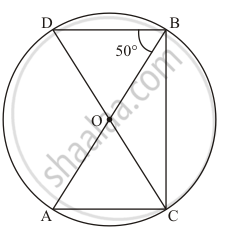
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
उत्तर
It is given that, AB and CD are diameter with center O and `angleOBD = 50°`
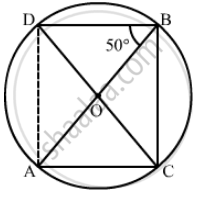
We have to find `angle AOC`
Construction: Join the point A and D to form line AD
Clearly arc AD subtends`angle ABD = 50°` at B and `angleAOD` at the centre.
Therefore,
Since CD is a straight line then
APPEARS IN
संबंधित प्रश्न
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
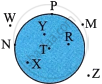 |
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
In the given figure, O is the centre of the circle. Name all chords of the circle.