Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circle. Find ∠CBD.

उत्तर
It is given that, `angle AOC = 100°`
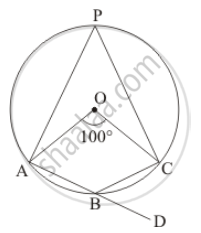
We have to find `angleCBD`
Since `angleAOC = 100°` (Given)
So,
`angleAPC = 1/2 angleAOC` (The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.)
`⇒ angleAPC = 1/2 xx 100`
= 50°
Now,
`angle APC + angleABC = 180° ` (Opposite pair of angle of cyclic quadrilateral)
So,
`50°+ angleABC = 180° `
`angleABC = 180° - 50°`
= 130°
⇒`angle ABC` = 130° …… (1)
`angle ABC + angleCBD = 180° ` (Linear pair)
`130° + angle CBD = 180° ( angleABC = 130)`
`angle CBD = 180° - 130° `
= 50°
Hence `angle CBD ` = 50°
APPEARS IN
संबंधित प्रश्न
Fill in the blank
A continuous piece of a circle is ............... of the circle
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
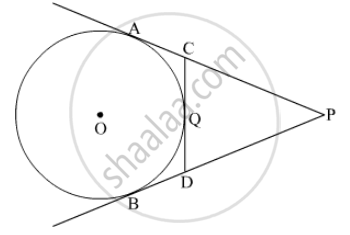

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
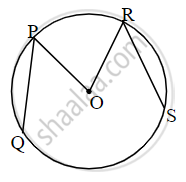
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
