Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle. Find ∠CBD.

Solution
It is given that, `angle AOC = 100°`
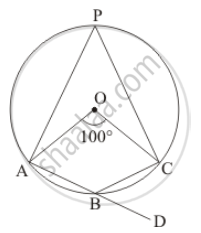
We have to find `angleCBD`
Since `angleAOC = 100°` (Given)
So,
`angleAPC = 1/2 angleAOC` (The angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.)
`⇒ angleAPC = 1/2 xx 100`
= 50°
Now,
`angle APC + angleABC = 180° ` (Opposite pair of angle of cyclic quadrilateral)
So,
`50°+ angleABC = 180° `
`angleABC = 180° - 50°`
= 130°
⇒`angle ABC` = 130° …… (1)
`angle ABC + angleCBD = 180° ` (Linear pair)
`130° + angle CBD = 180° ( angleABC = 130)`
`angle CBD = 180° - 130° `
= 50°
Hence `angle CBD ` = 50°
APPEARS IN
RELATED QUESTIONS
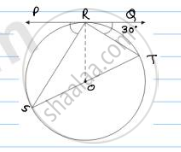
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

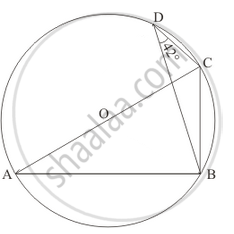
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
Is every diameter of a circle also a chord?
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
