Advertisements
Advertisements
Question
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
Solution

The circumference of the circular park = 352 m.
Let r be the radius of the circular park.
Then, 2πr = 352
`2 xx 22/7 xx r` = 352
r = `(352 xx 7)/(2 xx 22)` = 56 m
Area of circular park = πr2
= `22/7 xx (56)^2`
= `22/7 xx 56 xx 56`
= 22 × 8 × 56
= 9856 m2
Now, the circular park's radius with road,
R = 56 + 7 = 63 m
∴ Circular park area with a road
= πR2
= `22/7 xx (63)^2`
= `22/7 xx 63 xx 63`
= 22 × 9 × 63
= 12474 m2
So, Area of road = Area of circular park with road – Area of circular park
= 12474 – 9856
= 2618 m2
Hence, the area of road is 2618 m2.
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
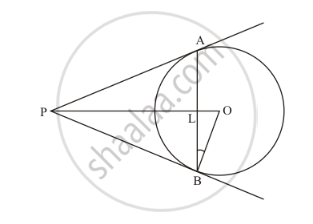
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In the given figure, ABC is a right triangle right-angled at B such that BC = 6 cm and AB = 8 cm. Find the radius of its incircle.

In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.


In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
If O is the centre of the circle, find the value of x in each of the following figures

Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
A line segment which joins any two points on a circle is a ___________
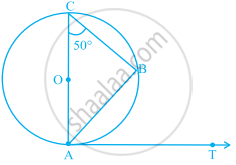
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
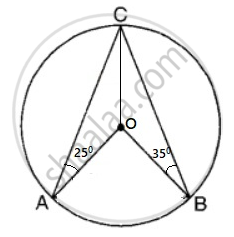
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

From the figure, identify a sector.

