Advertisements
Advertisements
Question
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

Solution
Given, ∠OAB = 30° and ∠OCB = 57°
In ΔAOB, AO = OB ...[Both are the radius of a circle]
⇒ ∠OBA = ∠BAO = 30° ...[Angles opposite to equal sides are equal]
In ΔAOB,
⇒ ∠AOB + ∠OBA + ∠BAO = 180° ...[By angle sum property of a triangle]
∴ ∠AOB + 30° + 30° = 180°
∴ ∠AOB = 180° – 2(30°)
= 180° – 60°
= 120° ...(i)
Now, in ΔAOB,
OC = OB ...[Both are the radius of a circle]
⇒ ∠OBC = ∠OCB = 57° ...[Angles opposite to equal sides are equal]
In ΔOCB,
∠COB + ∠OCB + ∠CBO = 180° ...[By angle sum property of triangle]
∴ ∠COB = 180° – (∠OCB + ∠OBC)
= 180° – (57° + 57°)
= 180° – 114°
= 66° ...(ii)
From equation (i), ∠AOB = 120°
⇒ ∠AOC + ∠COB = 120°
⇒ ∠AOC + 66° = 120° ...[From equation (ii)]
∴ ∠AOC = 120° – 66° = 54°
APPEARS IN
RELATED QUESTIONS
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
true or false
A circle is a plane figure.
true or false
Sector is the region between the chord and its corresponding arc.
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
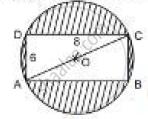
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
Draw circle with diameter: 6 cm
In above case, measure the length of the radius of the circle drawn.
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c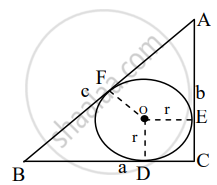
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

