Advertisements
Advertisements
प्रश्न
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

उत्तर
Given, ∠OAB = 30° and ∠OCB = 57°
In ΔAOB, AO = OB ...[Both are the radius of a circle]
⇒ ∠OBA = ∠BAO = 30° ...[Angles opposite to equal sides are equal]
In ΔAOB,
⇒ ∠AOB + ∠OBA + ∠BAO = 180° ...[By angle sum property of a triangle]
∴ ∠AOB + 30° + 30° = 180°
∴ ∠AOB = 180° – 2(30°)
= 180° – 60°
= 120° ...(i)
Now, in ΔAOB,
OC = OB ...[Both are the radius of a circle]
⇒ ∠OBC = ∠OCB = 57° ...[Angles opposite to equal sides are equal]
In ΔOCB,
∠COB + ∠OCB + ∠CBO = 180° ...[By angle sum property of triangle]
∴ ∠COB = 180° – (∠OCB + ∠OBC)
= 180° – (57° + 57°)
= 180° – 114°
= 66° ...(ii)
From equation (i), ∠AOB = 120°
⇒ ∠AOC + ∠COB = 120°
⇒ ∠AOC + 66° = 120° ...[From equation (ii)]
∴ ∠AOC = 120° – 66° = 54°
APPEARS IN
संबंधित प्रश्न
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
The length of three concesutive sides of a quadrilateral circumscribing a circle are 4 cm, 5 cm, and 7 cm respectively. Determine the length of the fourth side.
In the given circle with diameter AB, find the value of x.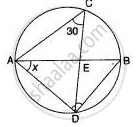
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.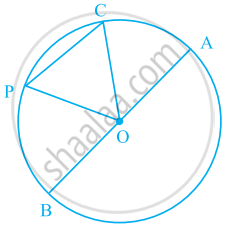
From the figure, identify a chord.

