Advertisements
Advertisements
प्रश्न
In the given circle with diameter AB, find the value of x.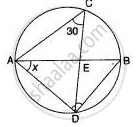
उत्तर
∠ ABD = ∠ ACD = 30° ....(∠s of same segment)
∠ADB = 90° ....(∠ in the semi circle)
In ΔADB,
x° + 90° + 30° = 180° ....(Sum of all ∠s of triangle)
x° = 180° - 120°
x° = 60°.
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
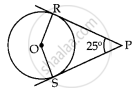
In the given figure, if ZRPS = 25°, the value of ZROS is ______
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
