Advertisements
Advertisements
प्रश्न
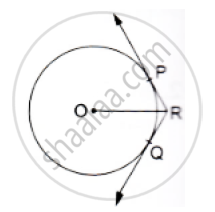
In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
उत्तर

Construction Join PO and OQ
In ΔPOR and ΔQOR
OP = OQ(Radii)
RP = RQ(Tangents from the external point are congruent)
OR = OR (Common)
By SSS congruency, ΔPOR ≅ ΔQOR
∠PRO = ∠QRO(C.P.C.T)
Now,∠PRO+ ∠QRO= ∠PRQ
⇒ 2 ∠PRO = 120°
⇒ ∠PRO = 60°
Now. In ΔPOR
cos 60° `=(PR)/(OR)`
⇒ `1/2 =(PR)/(OR)`
⇒ OR = 2PR
⇒ OR = PR + PR
⇒ OR = PR +RQ
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
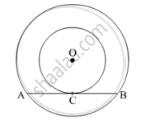
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
All the radii of a circle are _______________
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
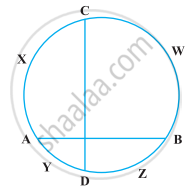
In the given figure, O is the centre of the circle. Name all chords of the circle.