Advertisements
Advertisements
प्रश्न
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
उत्तर
A and B are the two points that lie on the circle and O is the centre of the circle.
Therefore, OA and OB are the radii of the circle.
Using the distance formula, we have:
`OA=sqrt((-1-2)^2+(y+3y)^2)=sqrt(9+16y^2)`
`OB=sqrt((5-2)^2+(7+3y)^2)=sqrt(9+(7+3y)^2)`
Now, OB = OA (Radii of the same circle)
`sqrt(9+(7+3y)^2)=sqrt(9+16y^2)`
9+(7+3y)2=9+16y^2 (squaring both the sides)
49+9y2+42y=16y2
⇒7y2−42y−49=0
⇒y2−6y−7 =0
⇒y2−7y+y−7=0
⇒(y−7)(y+1)=0
⇒y−7=0 or y+1=0
⇒y=7 or y=−1
When y = 7:
Radius of the circle, `OA=sqrt(9+16y^2)=sqrt(9+16×49)=sqrt(793)`
When y = −1:
Radius of the circle, `OA=sqrt(9+16y^2) =sqrt(9+16×1)=sqrt(25)=5`
APPEARS IN
संबंधित प्रश्न
In fig., circles C(O, r) and C(O’, r/2) touch internally at a point A and AB is a chord of the circle C (O, r) intersecting C(O’, r/2) at C, Prove that AC = CB.
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
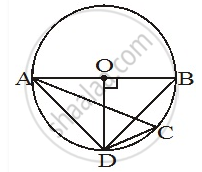
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
From the figure, identify a diameter.
Say true or false:
The centre of a circle is always in its interior.
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
