Advertisements
Advertisements
प्रश्न
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
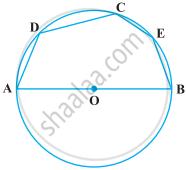
पर्याय
True
False
उत्तर
This statement is True.
Explanation:
Let AOB be the diameter of the circle.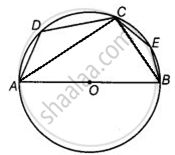
Given: ∠ADC = 120°
Firstly, join CB.
Then, we have a cyclic quadrilateral ABCD.
Since sum of opposite angles of cyclic quadrilateral is 180°, therefore
∠ADC + ∠ABC = 180°
⇒ 120° + ∠ABC = 180°
⇒ ∠ABC = 180° – 120°
⇒ ∠ABC = 60°
Now join AC.
Also, diameter subtends a right angle to the circle,
∴ In ΔABC, ∠ACB = 90°
Now, by angle sum property of a triangle, sum of all angles of a triangle is 180°.
∴ ∠CAB + ∠ABC + ∠ACB = 180°
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – 90° – 60°
⇒ ∠CAB = 30°
APPEARS IN
संबंधित प्रश्न
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
In the given circle with diameter AB, find the value of x.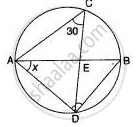
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
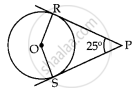
In the given figure, if ZRPS = 25°, the value of ZROS is ______
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
