Advertisements
Advertisements
Question
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.
Options
True
False
Solution
This statement is True.
Explanation:
Let AOB be the diameter of the circle.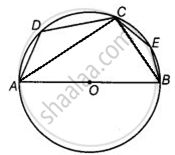
Given: ∠ADC = 120°
Firstly, join CB.
Then, we have a cyclic quadrilateral ABCD.
Since sum of opposite angles of cyclic quadrilateral is 180°, therefore
∠ADC + ∠ABC = 180°
⇒ 120° + ∠ABC = 180°
⇒ ∠ABC = 180° – 120°
⇒ ∠ABC = 60°
Now join AC.
Also, diameter subtends a right angle to the circle,
∴ In ΔABC, ∠ACB = 90°
Now, by angle sum property of a triangle, sum of all angles of a triangle is 180°.
∴ ∠CAB + ∠ABC + ∠ACB = 180°
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – 90° – 60°
⇒ ∠CAB = 30°
APPEARS IN
RELATED QUESTIONS
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
true or false
Sector is the region between the chord and its corresponding arc.
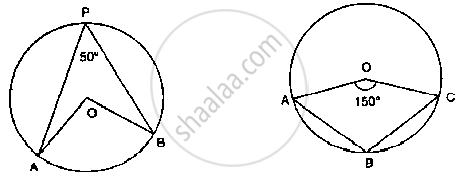
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
Find the length of tangent drawn to a circle with radius 8 cm form a point 17 cm away from the center of the circle
Use the figure given below to fill in the blank:
Diameter = 2 x ________

State, if the following statement is true or false:
The longest chord of a circle is its diameter.
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
From the figure, identify a point in the exterior.

