Advertisements
Advertisements
Question
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
Solution
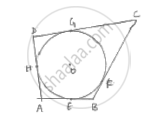
Let us consider a quadrilateral ABCD, AB = 4cm, BC = 5 cm, CD = 7cm, CD as sides
circumscribing circle with centre O. and intersecting at points E, F, G, H. as in fig.
We know that the tangents drawn from external point to the circle are equal in length.
From point A, AE = AH …. (i)
From point B, BE = BF ….. (ii)
From point C, GC = CE ….(iii)
From point D, GD = DH ….(iv)
(i) + (ii) + (iii) + (iv) ⇒ (AE + BE + GC + GD) = (AH + BF + CF + DH)
⇒ (AE + BE) + (GC + GD) = (AH + DH) + (BF + CF)
⇒ AB + CD = AD + BC
⇒ AD = 11 – 5 = 6 cm
Fourth side = 6 cm
APPEARS IN
RELATED QUESTIONS
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

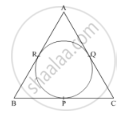
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.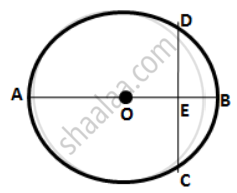
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
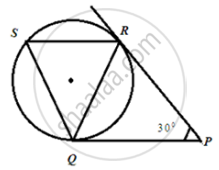
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.