Advertisements
Advertisements
Question
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.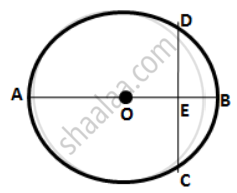
Solution
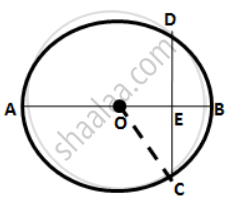
Let the radius of the circle be r cm.
∴ OE = OB - EB = r - 4
Join OC.
In right ΔOEC,
OC2 = OE2 + CE2
⇒ r2 = ( r - 4 )2 + (8)2
⇒ r2 = r2 - 8r + 16 + 64
⇒ 8r = 80
∴ r = 10 cm
Hence, radius of the circle is 10 cm.
APPEARS IN
RELATED QUESTIONS
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
In fig. a circle touches all the four sides of quadrilateral ABCD with AB = 6cm, BC = 7cm, CD = 4cm. Find AD.
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
If O is the centre of the circle, find the value of x in each of the following figures

Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
If an isosceles triangle ABC, in which AB = AC = 6 cm, is inscribed in a circle of radius 9 cm, find the area of the triangle.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
