Advertisements
Advertisements
प्रश्न
The figure given below shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm,
find the radius of the circle.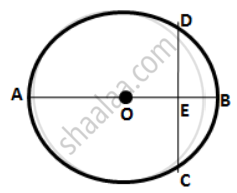
उत्तर
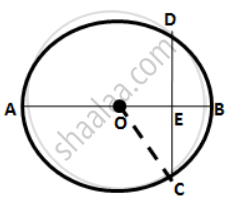
Let the radius of the circle be r cm.
∴ OE = OB - EB = r - 4
Join OC.
In right ΔOEC,
OC2 = OE2 + CE2
⇒ r2 = ( r - 4 )2 + (8)2
⇒ r2 = r2 - 8r + 16 + 64
⇒ 8r = 80
∴ r = 10 cm
Hence, radius of the circle is 10 cm.
APPEARS IN
संबंधित प्रश्न
Prove that there is one and only one tangent at any point on the circumference of a circle.
In the given figure, PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersects PQ at A and RS at B. Prove that ∠AOB = 90º
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
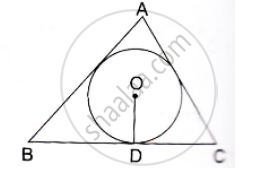
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
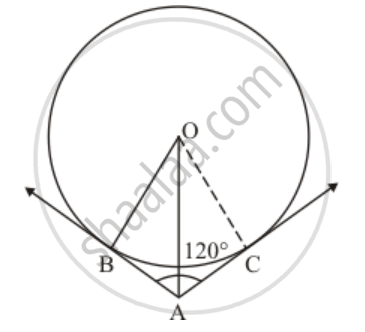
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
