Advertisements
Advertisements
प्रश्न
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
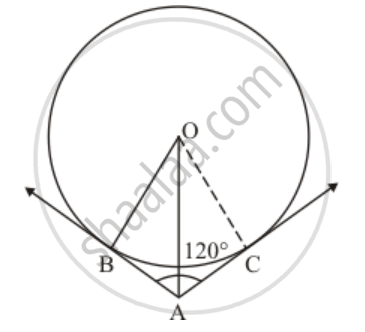
उत्तर
Consider Δ OAB and Δ OAC.
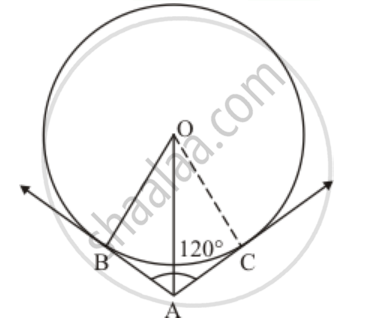
We have,
OB = OC (Since they are radii of the same circle)
AB = AC (Since length of two tangents drawn from an external point will be equal)
OA is the common side.
Therefore by SSS congruency, we can say that Δ OAB and Δ OAC are congruent triangles.
Therefore,
∠OAC = ∠OAC
It is given that,
`∠OAB +∠OAC=120^o`
`2∠OAB=120^o`
`∠OAB=60^o`
We know that,
`cos∠OAB =(AB)/(OA) `
`cos 60^o =(AB)/(OA) `
We know that,
`cos 60^o =1/2`
Therefore,
`1/2=(AB)/(OA)`
OA = 2AB
APPEARS IN
संबंधित प्रश्न
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7 cm.
Prove that the tangents at the extremities of any chord make equal angles with the chord.
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
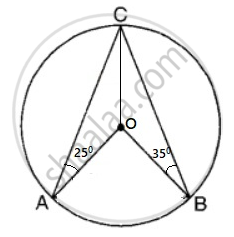
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
Is every chord of a circle also a diameter?
