Advertisements
Advertisements
प्रश्न
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
पर्याय
12 cm
12 cm
12 cm
18 cm
उत्तर
18 cm
We are given the chord of length 14 cm and perpendicular distance from the centre to the chord is 6 cm. We are asked to find the length of another chord at a distance of 2 cm from the centre.
We have the following figure
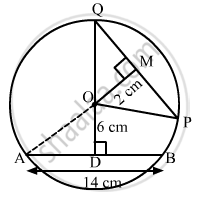
We are given AB = 14 cm, OD = 6 cm, MO = 2 cm, PQ = ?
Since, perpendicular from centre to the chord divide the chord into two equal parts
Therefore
`AQ^2 = AD^2 +OD^2`
= ` 7^2 + 6^2`
= 49 + 36
`= sqrt( 85)`
Now consider the ΔOPQ in which OM = 2 cm
So using Pythagoras Theorem in ΔOPM
`PM^2 = OP^2 -OM^2`
`=(sqrt(85))^2 - 2^2` (∵ OP = AO = radius)
= 81
= 9 cm
Hence PQ = 2 PM
= 2 × 9
= 18 cm
APPEARS IN
संबंधित प्रश्न
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
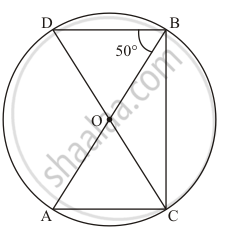
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
Say true or false:
Two diameters of a circle will necessarily intersect.
