Advertisements
Advertisements
प्रश्न
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
उत्तर
Given: An equilateral triangle ABC in which D, E, and F are the midpoints of sides BC, CA and AB respectively.
To prove: The centroid and circumference are coincident.
Construction: Draw medians AD, BE and CF.
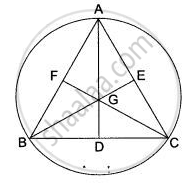
Proof:
Let G be the centroid of ΔABC i.e., the point of intersection of AD, BE, and CF. In triangles BEC and BFC, we have
∠ B = ∠ C = 60°
BC = BC
and BF = CE ...[ ∵ AB = AC ⇒
∴ ΔBEC = ΔBFC
⇒ BE = CF ...(i)
Similarly,
Δ CAF and Δ CAD
⇒ CF = AD ...(ii)
From (i) and (ii),
AD = BE = CF
⇒
CG =
GA =
GB =
GA = GB = GC
⇒ G is the equidistant from the vertices
⇒ G is the circumcentre of ΔABC.
Hence, the centroid and circumcentre are coincident.
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF =
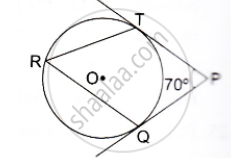
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
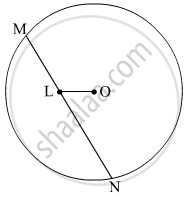
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Use the figure given below to fill in the blank:
If PQ is 8 cm long, the length of RS = ________

Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of the common chord PQ.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
