Advertisements
Advertisements
प्रश्न
In an equilateral triangle, prove that the centroid and center of the circum-circle (circumcentre) coincide.
उत्तर
Given: An equilateral triangle ABC in which D, E, and F are the midpoints of sides BC, CA and AB respectively.
To prove: The centroid and circumference are coincident.
Construction: Draw medians AD, BE and CF.
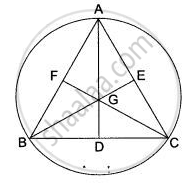
Proof:
Let G be the centroid of ΔABC i.e., the point of intersection of AD, BE, and CF. In triangles BEC and BFC, we have
∠ B = ∠ C = 60°
BC = BC
and BF = CE ...[ ∵ AB = AC ⇒ `1/2"AB" = 1/2` AC ⇒ BF = CE ]
∴ ΔBEC = ΔBFC
⇒ BE = CF ...(i)
Similarly,
Δ CAF and Δ CAD
⇒ CF = AD ...(ii)
From (i) and (ii),
AD = BE = CF
⇒ `2/3"AD" = 2/3 BE = 2/3"CF"`
CG = `2/3"CF"`
GA = `2/3"AD"`
GB = `2/3 "BE"`
GA = GB = GC
⇒ G is the equidistant from the vertices
⇒ G is the circumcentre of ΔABC.
Hence, the centroid and circumcentre are coincident.
APPEARS IN
संबंधित प्रश्न
n Fig. 2, PQ and PR are two tangents to a circle with centre O. If ∠QPR = 46°, then ∠QOR equals:
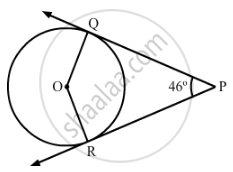
(A) 67°
(B) 134°
(C) 44°
(D) 46°
A chord PQ of a circle of radius 10 cm substends an angle of 60° at the centre of circle. Find the area of major and minor segments of the circle.
true or false
A circle is a plane figure.
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Can the length of a chord of a circle be greater than its diameter ? Explain.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

From the figure, identify the centre of the circle.
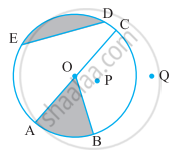
Say true or false:
The centre of a circle is always in its interior.
