Advertisements
Advertisements
प्रश्न
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

विकल्प
30º
60º
90º
45º
उत्तर
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to 45º.
Explanation:
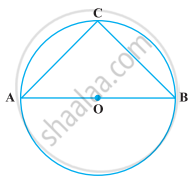
We know that, diameter subtends a right angle to the circle.
∴ ∠BCA = 90º ...(i)
Given, AC = BC
⇒ ∠ABC = ∠CAB ...(ii) [Angles opposite to equal sides are equal]
In ΔABC, ∠CAB + ∠ABC + ∠BCA = 180º ...[By angle sum property of a triangle]
⇒ ∠CAB + ∠CAB + ∠90º = 180º ...[From equations (i) and (ii)]
⇒ 2∠CAB = 180º – 90º
⇒ ∠CAB = `(90^circ)/2`
∴ ∠CAB = 45º
APPEARS IN
संबंधित प्रश्न
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
If O is the centre of the circle, find the value of x in each of the following figures

In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

From the figure, identify the centre of the circle.