Advertisements
Advertisements
प्रश्न
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

उत्तर
Let us consider, the points A, B, C and D form a cyclic quadrilateral.
∴ ∠ADC + ∠OBC = 180° ...[The sum of opposite angles of a cyclic quadrilateral is 180°]
`\implies` 130° + ∠OBC = 180°
`\implies` ∠OBC = 180° – 130° = 50°
In ΔBOC and ΔBOE,
BC = BE ...[Given]
OC = OE ...[Radii of a same circle]
And OB = OB ...[Common]
∴ ΔBOC ≅ ΔBOE ...[By SSS congruency]
`\implies` ∠OBC = ∠OBE ...[By C.P.C.T]
Now, ∠CBE = ∠CBO + ∠EBO
= 50° + 50°
= 100°
APPEARS IN
संबंधित प्रश्न
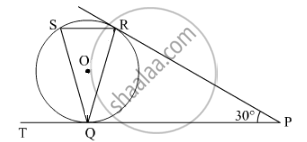
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
If ΔABC is isosceles with AB = AC and C (0, 2) is the in circle of the ΔABC touching BC at L, prove that L, bisects BC.
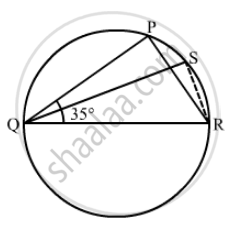
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
Use the figure given below to fill in the blank:
Diameter = 2 x ________

The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
The ratio between the circumference and diameter of any circle is _______
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
From the figure, identify a sector.

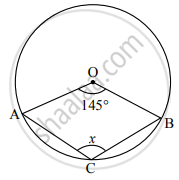
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.