Advertisements
Advertisements
प्रश्न
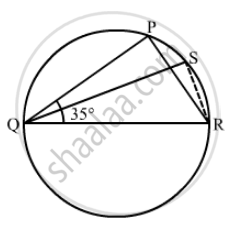
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
उत्तर
Disclaimer: Figure given in the book was showing m∠PQR as m∠SQR. It is given that ΔPQR is an isosceles triangle with PQ = PR and m∠PQR = 35°

We have to find the m∠QSR and m∠QTR
Since ΔPQR is an isosceles triangle
So ∠PQR = ∠PRQ = 35°
Then
`angle QPR = 180° - (anglePQR + anglePRQ)`
= 180° - (35° + 35°)
=180° - 70°
=110°
Since PQTR is a cyclic quadrilateral
So
`angleP + angleT = 180°`
`angle T = 180° - 110°`
= 70°
In cyclic quadrilateral QSRT we have
`angle S + angle T` = 180°
`angle S = 180° - 70°`
= 110°
Hence,
`m angleQSR `= 110° and `angleQTR` = 70°
APPEARS IN
संबंधित प्रश्न
In Fig. 1, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is :
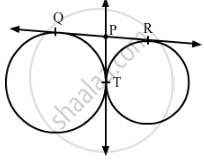
(A) 3.8
(B) 7.6
(C) 5.7
(D) 1.9
In Fig., if AB = AC, prove that BE = EC
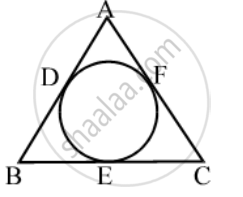
If the quadrilateral sides touch the circle prove that sum of pair of opposite sides is equal to the sum of other pair.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
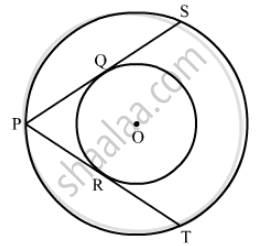
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
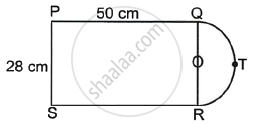
A figure is in the form of rectangle PQRS having a semi-circle on side QR as shown in the figure. Determine the area of the plot.