Advertisements
Advertisements
Question
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
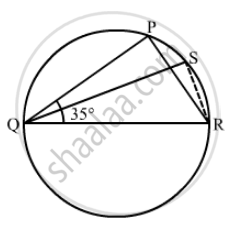
Solution
Disclaimer: Figure given in the book was showing m∠PQR as m∠SQR. It is given that ΔPQR is an isosceles triangle with PQ = PR and m∠PQR = 35°

We have to find the m∠QSR and m∠QTR
Since ΔPQR is an isosceles triangle
So ∠PQR = ∠PRQ = 35°
Then
`angle QPR = 180° - (anglePQR + anglePRQ)`
= 180° - (35° + 35°)
=180° - 70°
=110°
Since PQTR is a cyclic quadrilateral
So
`angleP + angleT = 180°`
`angle T = 180° - 110°`
= 70°
In cyclic quadrilateral QSRT we have
`angle S + angle T` = 180°
`angle S = 180° - 70°`
= 110°
Hence,
`m angleQSR `= 110° and `angleQTR` = 70°
APPEARS IN
RELATED QUESTIONS
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In a cyclic quadrilateral ABCD if AB || CD and ∠B = 70°, find the remaining angles.
A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
The circumcentre of a triangle is the point which is ______.
