Advertisements
Advertisements
Question
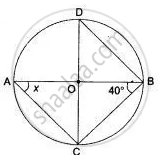
In the given figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

Solution
It is given that O is centre of the circle and ∠BOD = 160°
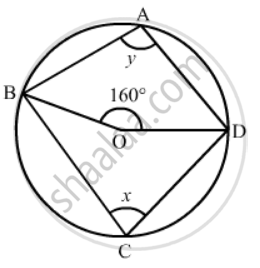
We have to find the values of x and y.
As we know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Therefore,
`x = 1/2 (160°)`
= 80°
Since, quadrilateral ABCD is a cyclic quadrilateral.
So,
x + y = 180° (Sum of opposite angles of a cyclic quadrilateral is 180°.)
` y = 180° - x`
=180° - 80°
= 100°
Hence `angle = 100° ` and `anglex = 80° `
APPEARS IN
RELATED QUESTIONS
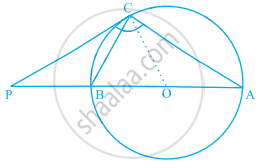
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
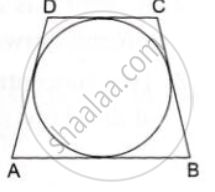
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
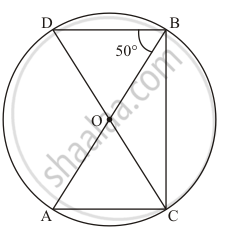
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
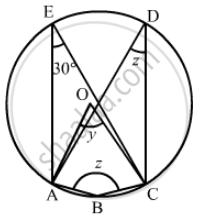
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
If O is the centre of the circle, find the value of x in each of the following figures
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
In a right triangle ABC in which ∠B = 90°, a circle is drawn with AB as diameter intersecting the hypotenuse AC and P. Prove that the tangent to the circle at P bisects BC.
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure