Advertisements
Advertisements
Question
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
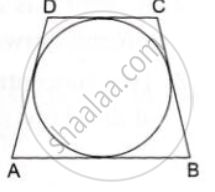
Solution
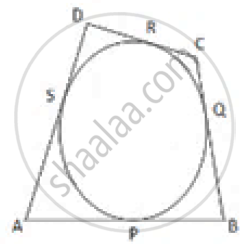
Let the circle touch the sides of the quadrilateral AB, BC, CD and DA at P, Q, R and S respectively.
Given, AB = 6cm, BC = 7 cm and CD = 4cm.
Tangents drawn from an external point are equal.
∴ AP = AS, BP = BQ,CR = CQ and DR = DS
Now, AB + CD (AP + BP) + (CR + DR)
⇒AB + CD= (AS+ BQ) + (CQ+ DS)
⇒ AB +CD +(AS+ DS) +(BQ+ CQ)
⇒ AB +CD =AD+ BC
⇒AD= ( AB+ CD)- BC
⇒ AD=(6+4)-7
⇒ AD = 3 cm.
∴ The length of AD is 3 cm.
APPEARS IN
RELATED QUESTIONS
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
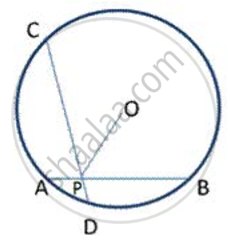
In the given figure, O is the centre of the circle. Find ∠CBD.

AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
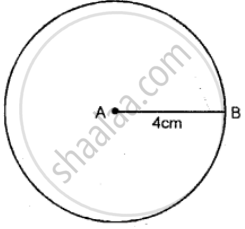
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
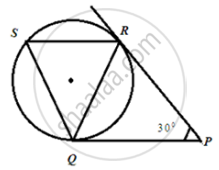
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
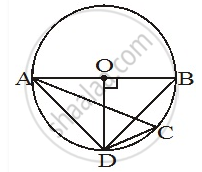
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
