Advertisements
Advertisements
Question
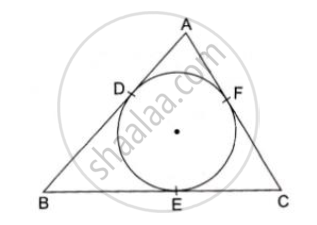
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
Solution
Sol:
We know that tangent segments to a circle from the same external point are congruent.
Now, we have
AD = AF, BD = BE and CE = CF
Now, AD + BD = l2cm …….(1)
AF + FC = l0 cm
⇒ AD + FC = l0 cm …….(2)
BE + EC = 8 cm
⇒ BD + FC = 8cm …….(3)
Adding all these we get
AD + BD + AD + FC + BD + FC = 30
⇒ 2(AD + BD + FC) = 30
⇒ AD + BD + FC = l5cm …….(4)
Solving (1) and (4), we get
FC = 3 cm
Solving (2) and (4), we get
BD = 5 cm
Solving (3) and (4), we get
and AD = 7 cm
∴ AD = AF =7 cm, BD = BE = 5 cm and CE = CF =3 cm
APPEARS IN
RELATED QUESTIONS
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
In Fig., if AB = AC, prove that BE = EC
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Can the length of a chord of a circle be greater than its diameter ? Explain.
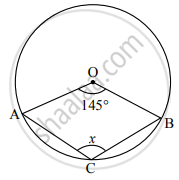
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.