Advertisements
Advertisements
Question
In Fig., if AB = AC, prove that BE = EC
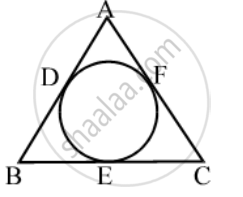
Solution
Since tangents from an exterior point to a circle are equal in length.
∴ AD = AF [Tangents from A]
BD = BE [Tangents from B]
CE = CF [Tangents from C]
Now,
AB = AC
⇒ AB – AD = AC – AD [Subtracting AD from both sides]
⇒ AB – AD = AC – AF [Using (i)]
⇒ BD = CF ⇒ BE = CF [Using (ii)]
⇒ BE = CE [Using (iii)]
APPEARS IN
RELATED QUESTIONS
true or false
A chord of a circle, which is twice as long is its radius is a diameter of the circle.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In the given figure, if ∠ABC = 45°, then ∠AOC =
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
