Advertisements
Advertisements
Question
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
Options
10 cm
9 cm
8 cm
6 cm
Solution
9 cm
Explanation;
Hint: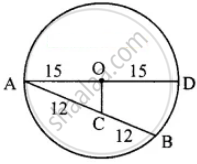
In ΔAOC,
AO = 15 cm
AC = `1/2` AB
= `1/2 xx 24`
= 12 cm
In ΔAOC,
OC2 = AO2 – AC2
= 152 – 122
= 225 – 144
= 81
OC = `sqrt(81)`
= 9 cm
APPEARS IN
RELATED QUESTIONS
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
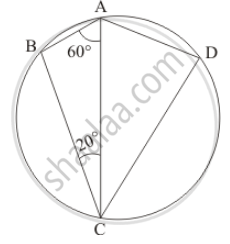
In the given figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure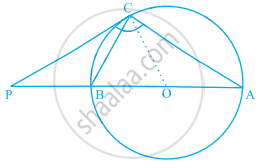
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

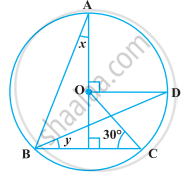
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
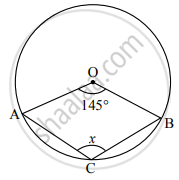
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.