Advertisements
Advertisements
Question
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

Options
30º
60º
90º
45º
Solution
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to 45º.
Explanation:
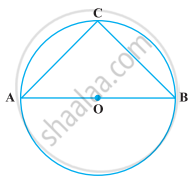
We know that, diameter subtends a right angle to the circle.
∴ ∠BCA = 90º ...(i)
Given, AC = BC
⇒ ∠ABC = ∠CAB ...(ii) [Angles opposite to equal sides are equal]
In ΔABC, ∠CAB + ∠ABC + ∠BCA = 180º ...[By angle sum property of a triangle]
⇒ ∠CAB + ∠CAB + ∠90º = 180º ...[From equations (i) and (ii)]
⇒ 2∠CAB = 180º – 90º
⇒ ∠CAB = `(90^circ)/2`
∴ ∠CAB = 45º
APPEARS IN
RELATED QUESTIONS
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
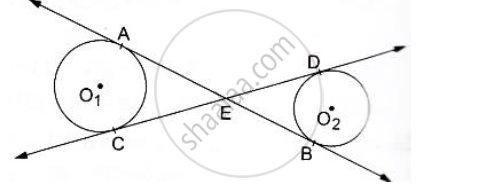
In the given figure common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB=CD
In the given figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB = 35°, then

In the given figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC + ∠ACD = 90°.

Use the figure given below to fill in the blank:
Tangent to a circle is _______.

The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
Say true or false:
The centre of a circle is always in its interior.
