Advertisements
Advertisements
Question
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
Options
`sqrt7` cm
7 cm
5 cm
25 cm
Solution
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is 5 cm.
Explanation:
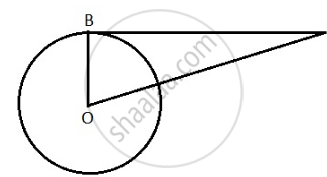
Given that AB = 4 cm, OB = 3 cm
To find OA
Applying Pythagoras theorem to triangle OAB
OB2 + AB2 = OA2
32 + 42 = OA
OA2 = 25
OA = 5 cm
Therefore the distance of A from the centre of the circle is 5 cm.
RELATED QUESTIONS
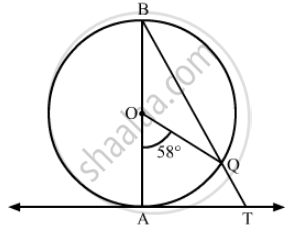
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.

Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
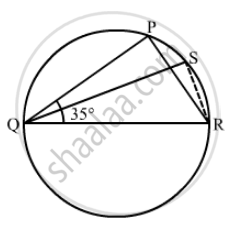
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides. Prove that ∠BAC = ∠BDC.
