Advertisements
Advertisements
Question
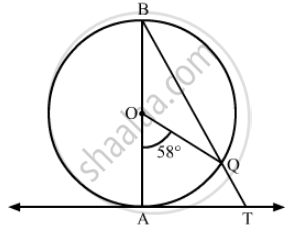
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
Solution
It is given that \[\angle\] AOQ = 58º.
We know that the angle subtended by an arc at the centre is twice the angle subtended by it any point on the remaining part of the circle.
∴\[\angle ABQ = \frac{1}{2}\angle AOQ = \frac{1}{2} \times 58^o = 29^o\]
Now, AT is the tangent and OA is the radius of the circle through the point of contact A.
In ∆ABT,
\[ \Rightarrow \angle ATB = 180^o - 119^o = 61^o\]
\[ \therefore \angle ATQ = \angle ATB = 61^o\]
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

ABCD is a quadrilateral such that ∠D = 90°. A circle (O, r) touches the sides AB, BC, CD and DA at P,Q,R and If BC = 38 cm, CD = 25 cm and BP = 27 cm, find r.
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
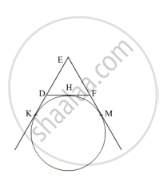
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.

Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
From the figure, identify three radii.