Advertisements
Advertisements
Question
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
Solution
Let the two circles intersect at points X and Y.
XY is the common chord.
Suppose ‘A’ is a point on the common chord and AM and AN be the tangents drawn A to the circle
We need to show that AM = AN.
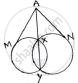
In order to prove the above relation, following property will be used.
“Let PT be a tangent to the circle from an external point P and a secant to the circle through
P intersects the circle at points A and B, then ๐๐2 = ๐๐ด × ๐๐ต"
Now AM is the tangent and AXY is a secant ∴ ๐ด๐2 = ๐ด๐ × ๐ด๐ … . . (๐)
AN is a tangent and AXY is a secant ∴ ๐ด๐2 = ๐ด๐ × ๐ด๐ … . . (๐๐)
From (i) & (ii), we have ๐ด๐2 = ๐ด๐2
∴ AM = AN
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.
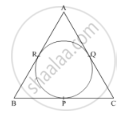
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
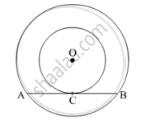
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
One chord of a circle is known to be 10 cm. The radius of this circle must be
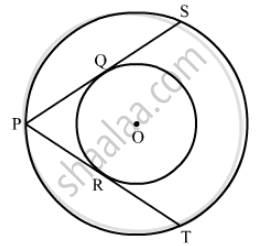
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
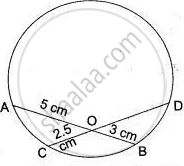
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
A line segment which joins any two points on a circle is a ___________
In figure, chords AC and DE intersect at B. If ∠ABE = 108°, m(arc AE) = 95°, find m(arc DC).
A line through the point of contact and passing through centre of the circle is known as ______
