Advertisements
Advertisements
Question
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

Solution
Construction: Join OB
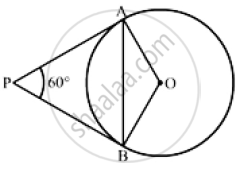
We know that the radius and tangent are perpendicular at their point of contact
∵ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB +∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB +90° + 60° + 90° = 360°
⇒ 240° + ∠AOB = 360°
⇒ ∠ AOB = 120°
Now, In isosceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180° [Angle sum property of a triangle]
⇒ 120° + 2 ∠OAB =180° [∵ ∠OAB = ∠OBA]
⇒ ∠OAB = 30°
APPEARS IN
RELATED QUESTIONS
Prove that two different circles cannot intersect each other at more than two points.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
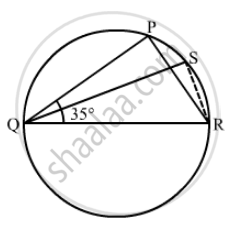
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
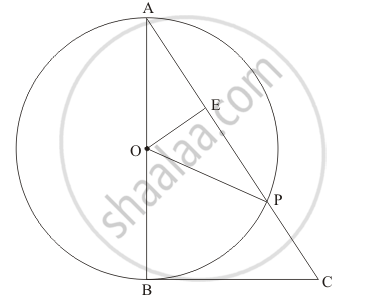
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.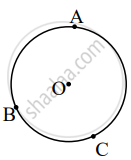
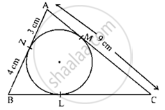
In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
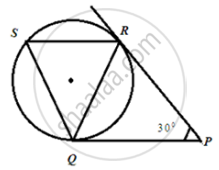
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
