Advertisements
Advertisements
Question
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

Solution
We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OPT = 90°
Now,∠OPQ = ∠OPT - ∠QPT = 90° - 60° = 30°
Since, OP = OQas born is radius
∴ ∠OPQ = ∠OQP = 30° (Angles opposite to equal sides are equal)
Now, In isosceles, POQ
∠POQ + ∠OPQ +∠OQP = 180° (Angle sum property of a triangle)
⇒ ∠POQ =180° - 30° - 30° =120°
Now, ∠POQ + reflex ∠POQ = 360° (Complete angle)
⇒ reflex ∠POQ = 360° - 120° = 240°
We know that the angle subtended by an arc at the centre double the angle subtended by the arc at any point on the remaining part of the circle
∴ ∠PRQ `=1/2 `( reflex ∠POQ)= 120°
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
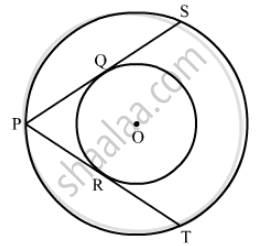
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
In the figure, O is the centre of a circle and diameter AB bisects the chord CD at a point E such that CE = ED = 8 cm and EB = 4 cm. The radius of the circle is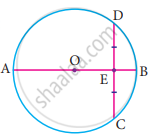
A line segment joining any point on the circle to its center is called the _____________ of the circle
