Advertisements
Advertisements
Question
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
Solution

Given
O is Centre of circle
PA and PB are tangents
We know that
The tangents drawn from external point to the circle are equal in length.
From point P, PA = PB
⇒ PL + AL = PN + NB …. (i)
From point L & N, AL = LM and MN = NB } …. Substitute in (i)
PL + Lm = PN + MN
⇒ Hence proved.
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
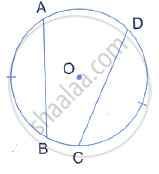
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
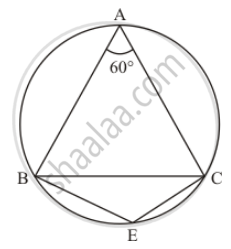
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
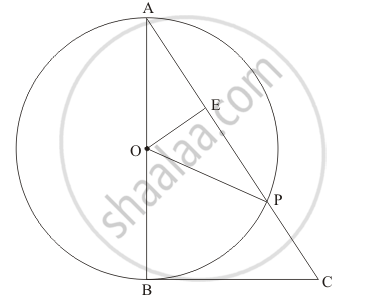
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
The ______________ is the longest chord of a circle
Twice the radius is ________________
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

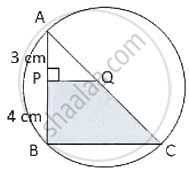
In the adjoining figure, AC is a diameter of the circle. AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ΔAPQ is 18 cm2, then the area of shaded portion QPBC is ______.