Advertisements
Advertisements
Question
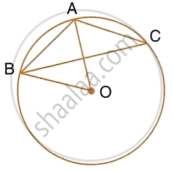
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
Solution
i. Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ `∠ACB = 1/2∠AOB`
Since AB is the side of a regular hexagon,
∠AOB = 60°
ii. `∠AOB = 60^circ => ∠ACB = 1/2 xx 60^circ = 30^circ`
iii. Since AC is the side of a regular octagon,
`∠AOC = 360^circ/8 = 45^circ`
Again, Arc AC subtends ∠AOC at the center and ∠ABC at the remaining part of the circle.
`=> ∠ABC = 1/2 ∠AOC`
`=> ∠ABC = 45^circ/2 = 22.5^circ`
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
Write True or False. Give reason for your answer.
A circle is a plane figure.
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

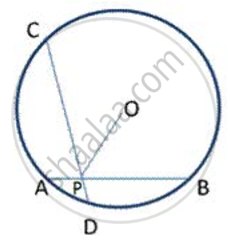
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 15 cm |
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
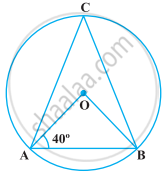
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.