Advertisements
Advertisements
Question
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

Solution
It is given that, O is the centre of the circle and \[\angle DAB = 50° \]
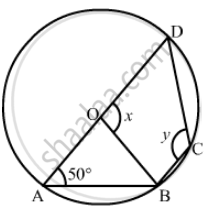
We have to find the values of x and y.
ABCD is a cyclic quadrilateral and `angle A + angle C = 180°`
So,
50° + y = 180°
y = 180° − 50°
y = 130°
Clearly Δ OAB is an isosceles triangle with OA = OB and `angle OBA = angle OAB`
Then, `angle OBA + angleOAB + angle AOB = 180°`
`angleAOB = 180° - ( 50° + 50° ) ` (Since `angleOBA = angle OAB = 50°` )
So, `angleAOB = 80°`
x + `angle AOB ` = 180° (Linear pair)
Therefore, x = 180° − 80° = 100°
Hence,
x = 100° and y = 130°
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Write True or False. Give reason for your answer.
Line segment joining the centre to any point on the circle is a radius of the circle.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

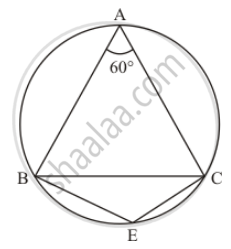
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Draw circle with the radii given below.
3 cm
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
