Advertisements
Advertisements
Question
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Solution
O is the centre of the circle.
chord PQ ≅ chord RS (Given)
⇒ arc PQ ≅ arc RS (Correspondidng arcs of congruent chords of a circle are congruent)
⇒ m(arc PQ) = m(arc RS)
⇒ m(arc PQ) = 80º [m(arc RS) = 80º]
(1)
m(arc PR) = ∠POR = 70º (Measure of a minor arc is the measure of its central angle)
(2)
m(arc PR) + m(arc PQ) + m(arc QS) + m(arc RS) = 360º
⇒ 70º + 80º + m(arc QS) + 80º = 360º
⇒ m(arc QS) = 360º − 230º = 130º
(3)
m(arc QSR) = m(arc QS) + m(arc RS) = 130º + 80º = 210º
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
Write True or False. Give reason for your answer.
Sector is the region between the chord and its corresponding arc.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

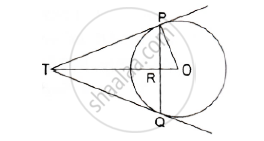
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
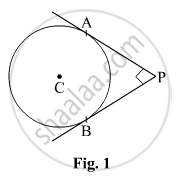
In Fig. 1, PA and PB are two tangents drawn from an external point P to a circle with centre C and radius 4 cm. If PA ⊥ PB, then the length of each tangent is:
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
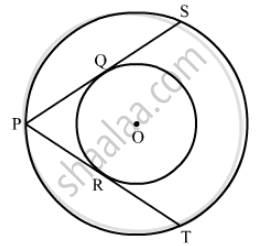
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC at P and OA at Q.
Prove that:
( i ) ΔOPA ≅ ΔOQC
( ii ) ΔBPC ≅ ΔBQA
Draw a circle of diameter 7 cm. Draw two radii of this circle such that the angle between these radii is 90°. Shade the minor sector obtained. Write a special name for this sector.
If the radius of a circle is 5 cm, what will its diameter be?
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
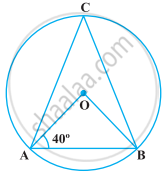
In the following figure, if ∠OAB = 40º, then ∠ACB is equal to ______.
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
From the figure, identify the centre of the circle.
From the figure, identify a segment.

