Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

उत्तर
O is the centre of the circle.
chord PQ ≅ chord RS (Given)
⇒ arc PQ ≅ arc RS (Correspondidng arcs of congruent chords of a circle are congruent)
⇒ m(arc PQ) = m(arc RS)
⇒ m(arc PQ) = 80º [m(arc RS) = 80º]
(1)
m(arc PR) = ∠POR = 70º (Measure of a minor arc is the measure of its central angle)
(2)
m(arc PR) + m(arc PQ) + m(arc QS) + m(arc RS) = 360º
⇒ 70º + 80º + m(arc QS) + 80º = 360º
⇒ m(arc QS) = 360º − 230º = 130º
(3)
m(arc QSR) = m(arc QS) + m(arc RS) = 130º + 80º = 210º
APPEARS IN
संबंधित प्रश्न
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
Fill in the blank
A continuous piece of a circle is ............... of the circle
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of another chord.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

In fig. 3 are two concentric circles of radii 6 cm and 4 cm with centre O. If AP is a tangent to the larger circle and BP to the smaller circle and length of AP is 8 cm, find the length of BP ?

In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Length of a chord of a circle is 24 cm. If distance of the chord from the centre is 5 cm, then the radius of that circle is ______.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.


In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 60°, then OP = `asqrt(3)`
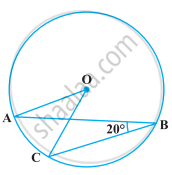
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
