Advertisements
Advertisements
प्रश्न
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
उत्तर
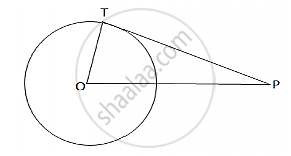
Draw a circle and let P be a point such that OP = 25cm.
Let TP be the tangent, so that TP = 24cm
Join OT where OT is radius.
Now, tangent drawn from an external point is perpendicular to the radius at the point of contact.
∴ OT ⊥ PT
In the right Δ OTP,we have:
`OP^2 = OT^2 +TP^2 ` [By Pythagoras’ theorem:]
`OT^2 = sqrt(OP^2 - TP^2 )`
`=sqrt(25^2 - 24^2`
`= sqrt(625-576)`
`=sqrt(49)`
= 7 cm
∴ The length of the radius is 7cm.
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
Fill in the blank
A continuous piece of a circle is ............... of the circle
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
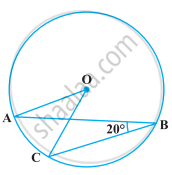
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
