Advertisements
Advertisements
प्रश्न
Let s denote the semi-perimeter of a triangle ABC in which BC = a, CA = b, AB = c. If a circle touches the sides BC, CA, AB at D, E, F, respectively, prove that BD = s – b.
उत्तर
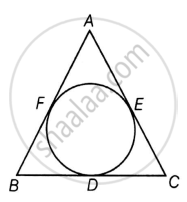
A triangle ABC with BC = a, CA = b and AB = c.
Also, a circle is inscribed, which touches the sides BC, CA and AB at D, E and F, respectively and s is semi-perimeter of the triangle
To Prove: BD = s – b
Proof:
We have,
Semi Perimeter = s
Perimeter = 2s
2s = AB + BC + AC ...[1]
As we know,
Tangents drawn from an external point to a circle are equal
So we have
AF = AE ...[2] [Tangents from point A]
BF = BD ...[3] [Tangents from point B]
CD = CE ...[4] [Tangents from point C]
Adding [2] [3] and [4]
AF + BF + CD = AE + BD + CE
AB + CD = AC + BD
Adding BD both side
AB + CD + BD = AC + BD + BD
AB + BC – AC = 2BD
AB + BC + AC – AC – AC = 2BD
2s – 2AC = 2BD ...[From 1]
2BD = 2s – 2b ...[As AC = b]
BD = s – b
Hence proved.
APPEARS IN
संबंधित प्रश्न
In figure PA and PB are tangents from an external point P to the circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
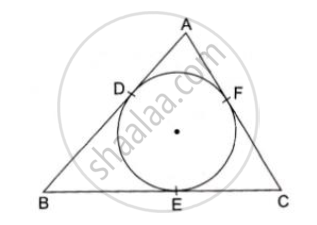
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
In the given figure, the area enclosed between the two concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, calculate the radius of the inner circle.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure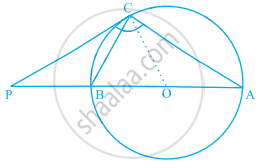
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
