Advertisements
Advertisements
प्रश्न
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
उत्तर
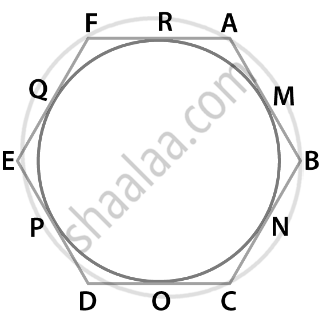
According to the question,
A Hexagon ABCDEF circumscribe a circle.
To prove: AB + CD + EF = BC + DE + FA
Proof: Tangents drawn from an external point to a circle are equal.
Hence, we have
AM = RA ...Equation 1 [tangents from point A]
BM = BN ...Equation 2 [tangents from point B]
CO = NC ...Equation 3 [tangents from point C]
OD = DP ...Equation 4 [tangents from point D]
EQ = PE ...Equation 5 [tangents from point E]
QF = FR ...Equation 6 [tangents from point F] [equation 1] + [equation 2] + [equation 3] + [equation 4] + [equation 5] + [equation 6]
AM + BM + CO + OD + EQ + QF = RA + BN + NC + DP + PE + FR
On rearranging, we get,
(AM + BM) + (CO + OD) + (EQ + QF) = (BN + NC) + (DP + PE) + (FR + RA)
AB + CD + EF = BC + DE + FA
Hence Proved!
APPEARS IN
संबंधित प्रश्न
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

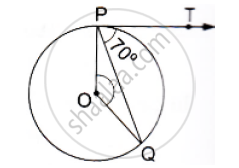
If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
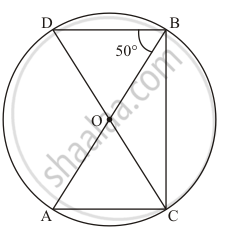
In the given figure, AB and CD are diameters of a circle with centre O. If ∠OBD = 50°, find ∠AOC.
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Use the figure given below to fill in the blank:
______ is a chord of the circle.

Use the figure given below to fill in the blank:
________ is a radius of the circle.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.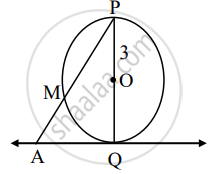
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
From the figure, identify two points in the interior.

