Advertisements
Advertisements
Question
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
Solution
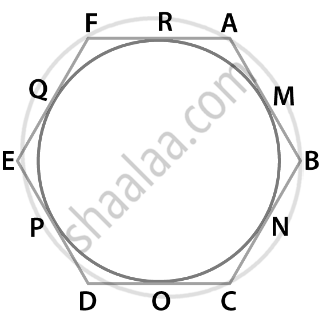
According to the question,
A Hexagon ABCDEF circumscribe a circle.
To prove: AB + CD + EF = BC + DE + FA
Proof: Tangents drawn from an external point to a circle are equal.
Hence, we have
AM = RA ...Equation 1 [tangents from point A]
BM = BN ...Equation 2 [tangents from point B]
CO = NC ...Equation 3 [tangents from point C]
OD = DP ...Equation 4 [tangents from point D]
EQ = PE ...Equation 5 [tangents from point E]
QF = FR ...Equation 6 [tangents from point F] [equation 1] + [equation 2] + [equation 3] + [equation 4] + [equation 5] + [equation 6]
AM + BM + CO + OD + EQ + QF = RA + BN + NC + DP + PE + FR
On rearranging, we get,
(AM + BM) + (CO + OD) + (EQ + QF) = (BN + NC) + (DP + PE) + (FR + RA)
AB + CD + EF = BC + DE + FA
Hence Proved!
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
A circle divides the plane, on which it lies, in __________ parts.
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
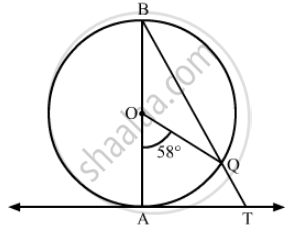
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Find the diameter of the circle
Radius = 10 cm
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
