Advertisements
Advertisements
प्रश्न
If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.
उत्तर
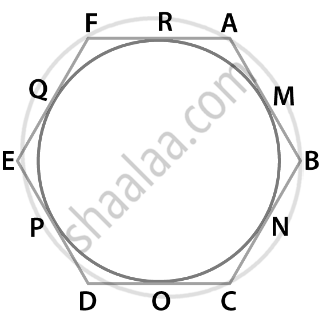
According to the question,
A Hexagon ABCDEF circumscribe a circle.
To prove: AB + CD + EF = BC + DE + FA
Proof: Tangents drawn from an external point to a circle are equal.
Hence, we have
AM = RA ...Equation 1 [tangents from point A]
BM = BN ...Equation 2 [tangents from point B]
CO = NC ...Equation 3 [tangents from point C]
OD = DP ...Equation 4 [tangents from point D]
EQ = PE ...Equation 5 [tangents from point E]
QF = FR ...Equation 6 [tangents from point F] [equation 1] + [equation 2] + [equation 3] + [equation 4] + [equation 5] + [equation 6]
AM + BM + CO + OD + EQ + QF = RA + BN + NC + DP + PE + FR
On rearranging, we get,
(AM + BM) + (CO + OD) + (EQ + QF) = (BN + NC) + (DP + PE) + (FR + RA)
AB + CD + EF = BC + DE + FA
Hence Proved!
APPEARS IN
संबंधित प्रश्न
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
ture or false v
The degree measure of a semi-circle is 180°.
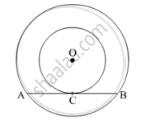
In Fig. 5, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

The radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
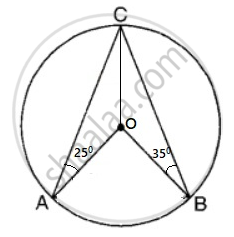
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
