Advertisements
Advertisements
Question
Find the diameter of the circle if the length of a chord is 3.2 cm and itd distance from the centre is 1.2 cm.
Solution
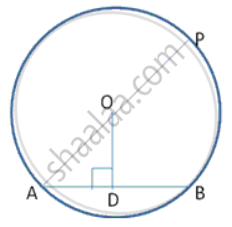
AD = DB = 1.6 cm (Perpendicular from centre to a chord bisects the chord)
In right Δ ODA ,
By Pythagoras theorem , OA2 = OD2 + AD2
= 1.62 + 1.22
= 2.56 + 1.44
OA2 = 4
OA = 2 cm
Diameter (AP) = 2 (OA) = 2 (1) = 4 cm
APPEARS IN
RELATED QUESTIONS
PA and PB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
Fill in the blank
A continuous piece of a circle is ............... of the circle
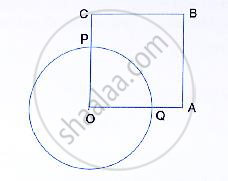
In the following figure, OABC is a square. A circle is drawn with O as centre which meets OC
at P and OA at Q. Prove that:
(i) ΔOPA ≅ ΔOQC, (ii) ΔBPC ≅ ΔBQA.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c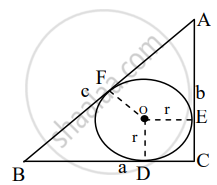
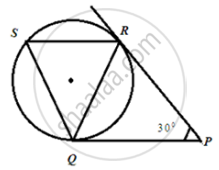
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
